- 学术相关
- 娱乐
- Quantifying Information Distribution in Social Networks: The Structural Entropy Index of Community (SEIC) for Twitter Communication Analysis
- Proximity to explosive synchronization determines network collapse and recovery trajectories in neural and economic crises
- Discovering sensorimotor agency in cellular automata using diversity search
- Survival Tips
学术相关
Modeling earth-scale human-like societies with one billion agents 1
Work in prgress.
这篇文章名字起得很大,但目前工作深度远远达不到这个名字的程度。它重点要解决的问题应该是如何降低大规模仿真的成本问题,作者提出了几个策略,并在观念传播网络中的f图中进行了token消耗比较,但作者没有提供细节和深入分析。作者重点说明了社会仿真结果与实际社会互动特征接近,我不认同这类验证LLMs仿真的方法,我认为这种特征有源自模型语料库训练导致数据泄漏的嫌疑,应该充分测试(如控制训练数据或比较大量不相关的特征指标排除模型根据操作者意愿生成数据的可能)并设计标准后才能作为仿真效果评估依据。
仿真系统设计
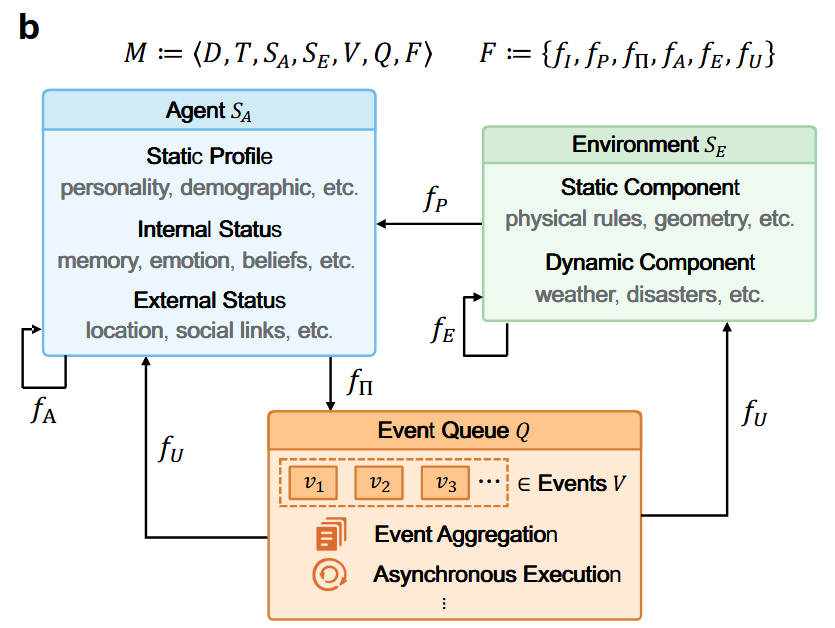
社会互动有智能体与环境状态的交互进行建模,通过事件队列进行调度
- 社会模型$M:=<D,T,S_A,S_E, V,Q,F>$
- $D$ Seed Dataset 种子数据集
- $T$模拟的时间线
- 每个时间步社会模型系统保有动态的激活智能体合集(出生、死亡、动作)
- 智能体状态$S_A$
- 静态配置(人口统计特征、个体特性等)
- 动态内部状态(记忆、信念、目标等)
- 动态外部状态(位置、社会连接等)
- 环境状态$S_E$
- 静态组件(空间布局、体制结构等)
- 动态组件(模拟进度如天气状况、灾难等)
- 事件$v\in \mathcal{V}$ 引导模拟动态变化
- 每个事件封装了系统中的离散交互或变化,例如代理发送消息、移动、形成关系等,每个事件包含优先级属性,被被存储在事件队列$Q$ 调度
- LLMs 驱动的模拟操作函数$F$
- 提供仿真系统的核心动态
- $f_I$ 基于种子数据集$D$ 初始化环境和智能体
- $f_P$ 智能体感知周边环境函数
- $f_\Pi$ 智能体决策和行为的政策操作函数
- $f_A$ 智能体随时间演化函数
- $f_E$ 环境随时间演化函数
- $f_U$ 更新操作函数
自动复杂混合模型框架
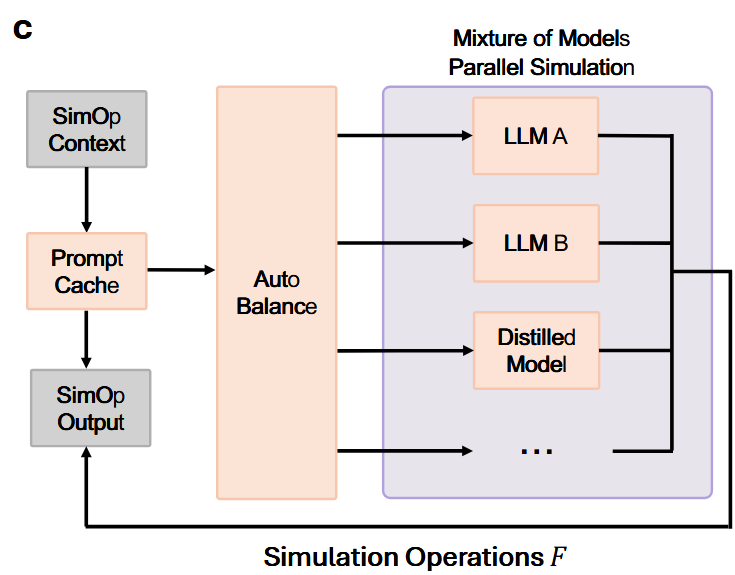
为降低大规模仿真的开销,本文使用了多层优化的方案:
- 语义提示词缓存机制
- 降低相似结构提示词的冗余开销
- 每次提示词查询都会被转换为向量并被存储
- 每次查询会首先进行相似检索,决定复用或使用新的提示词
- 周期性知识蒸镏训练任务专属模型
- 通过混合模型架构调度资源
- 根据保真度需求和资源可用性分配到完整LLM、蒸镏模型或其他模型
- 运行层面使用分布式和压缩图结构实现高效并发
实验结果
社会信任游戏
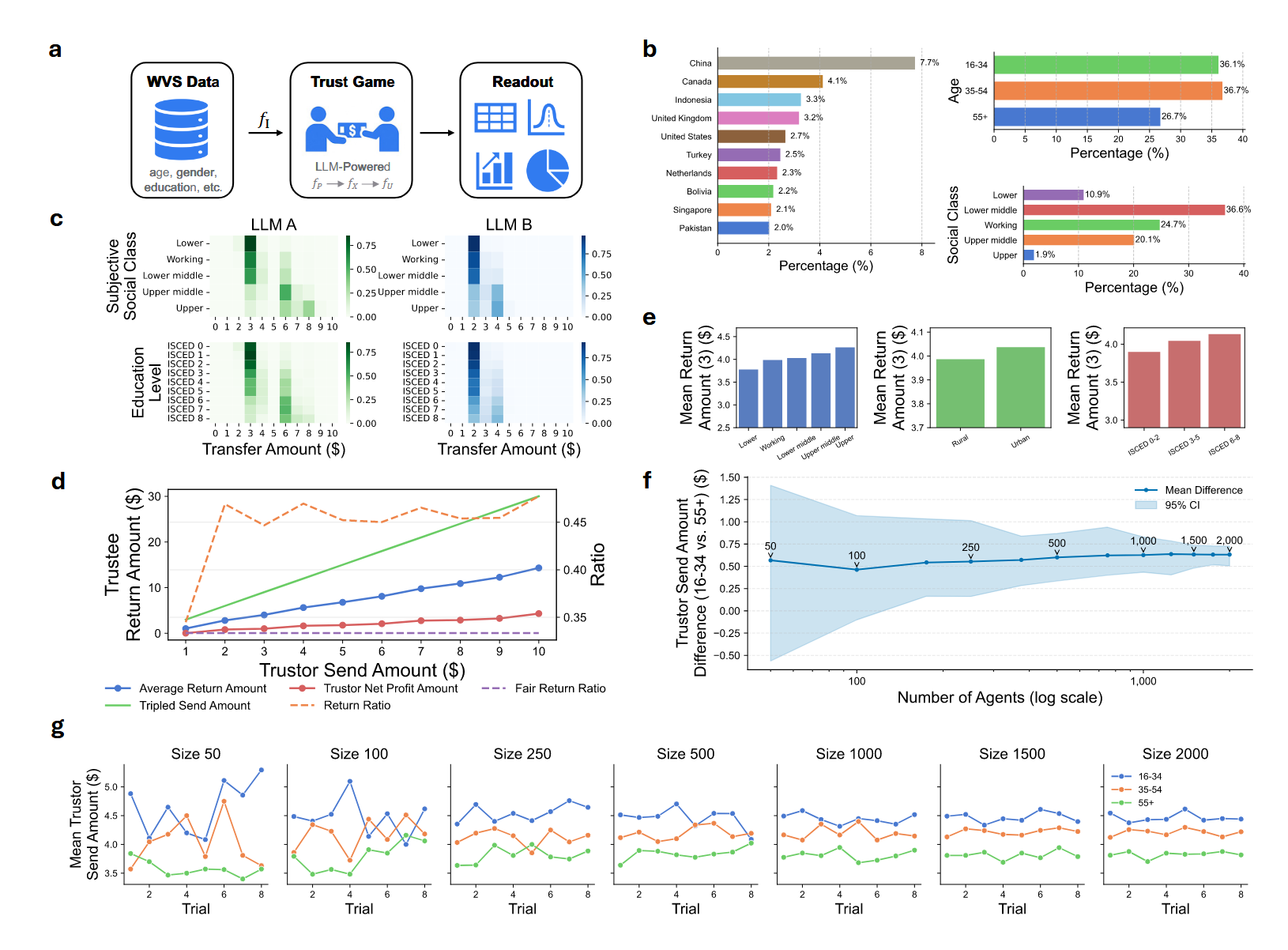
观念传播网络
基于Barabasi-Albert模型的仿真
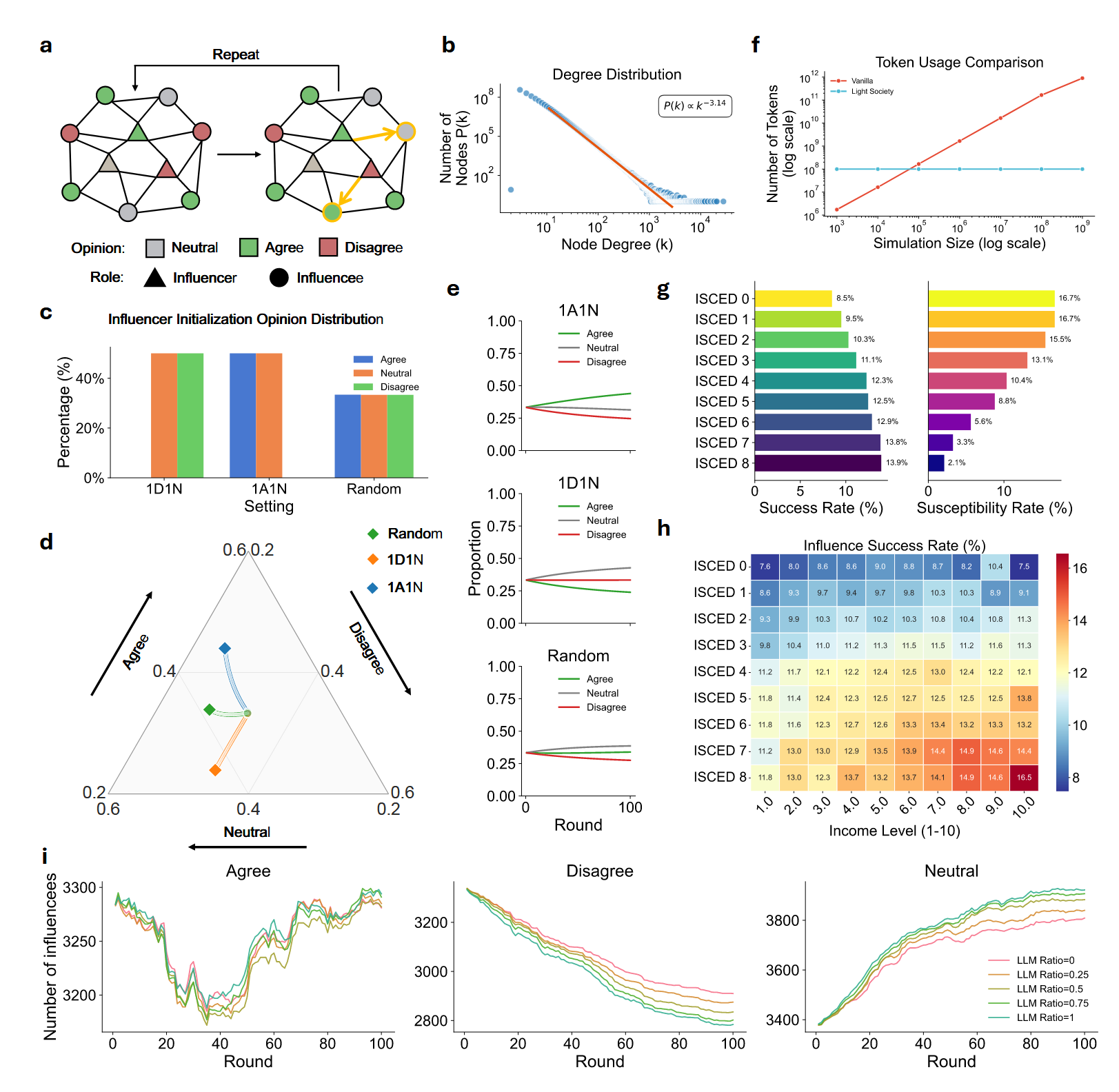
f图显示作者提出的架构Token消耗量几乎不随仿真规模增长而增长,但没有细节和详细解释。初步猜测应该包含大量高度同质化的智能体,通过缓存机制复用。
Intersectional inequalities in social ties 2
这篇文章有一部分没有读明白,模型整体设计比较复杂,但是我没有理解模型对结论有多大的贡献
以往的研究探讨了一维身份对社会连接差异的影响,但当多重身份交汇时,社会网络劣势会非线性积累,不成比例地伤害属于多个弱势群体的个体
这篇研究希望量化研究多维属性交互如何影响社会资本的多维和交叉不平等
作者提及的几种不适用的方法:
- 多层指数随机图模型ERGMs
- 用于分析多层网络中不同关系类型之间的依赖
- 多层随机块模型SBMs
- 用于识别网络中社群结构的概率生成模型
- 随机行动者导向模型SAOM
- 将网络视为由个体行动者决策驱动的连续时间随机过程
操作化
- 节点$i$属于一个用多维向量属性定义的D维社会小组
$s\in \mathcal{S}=S_1\times S_2\times\cdots\times S_D={1,\cdots,v_1}\times{1,\cdots,v_2}\times\cdots\times{1,\cdots,v_D}$
$s^d\in{1,\cdots,v_d}$是$i$在维度$d$的属性,它有$v_d$个不同潜在值
$\therefore 共计n_{mg}=\prod_{d=1}^D v_d个多维群体$
总体分布编码为张量$F$,其每个元素$F_{s_1,s_2,\cdots,s_D}$表示在多维群体中属于特定多维组$s=(s_1,s_2,\cdots,s_D)$的个体所占比例;$\sum_{s_1,s_2,\cdots,s_D}F_{s_1,s_2,\cdots,s_D}=1$
- 每个节点与每个维度存在潜在连接偏好,使用D 个同质性/ 异质性矩阵$h_d$编码,若第$d$个维度上有$n_d$个类别,则第$d$个矩阵的维度是$n_d\times n_d$
为生成一个有向图网络,从总体分布$F$中选取固定的一组$N$个节点及属性向量,之后选取一个节点$i$和$j$的随机对 。假设节点$i$属于多维群体组$r$,节点$j$属于$s$,则$i$的潜在偏好为${h_{r^d,s^d}^d; d=1,2,\cdots,D}$,$H_{r,s}=\prod_{d=1}^D h_{r^d,s^d}^d$决定两节点是否连接
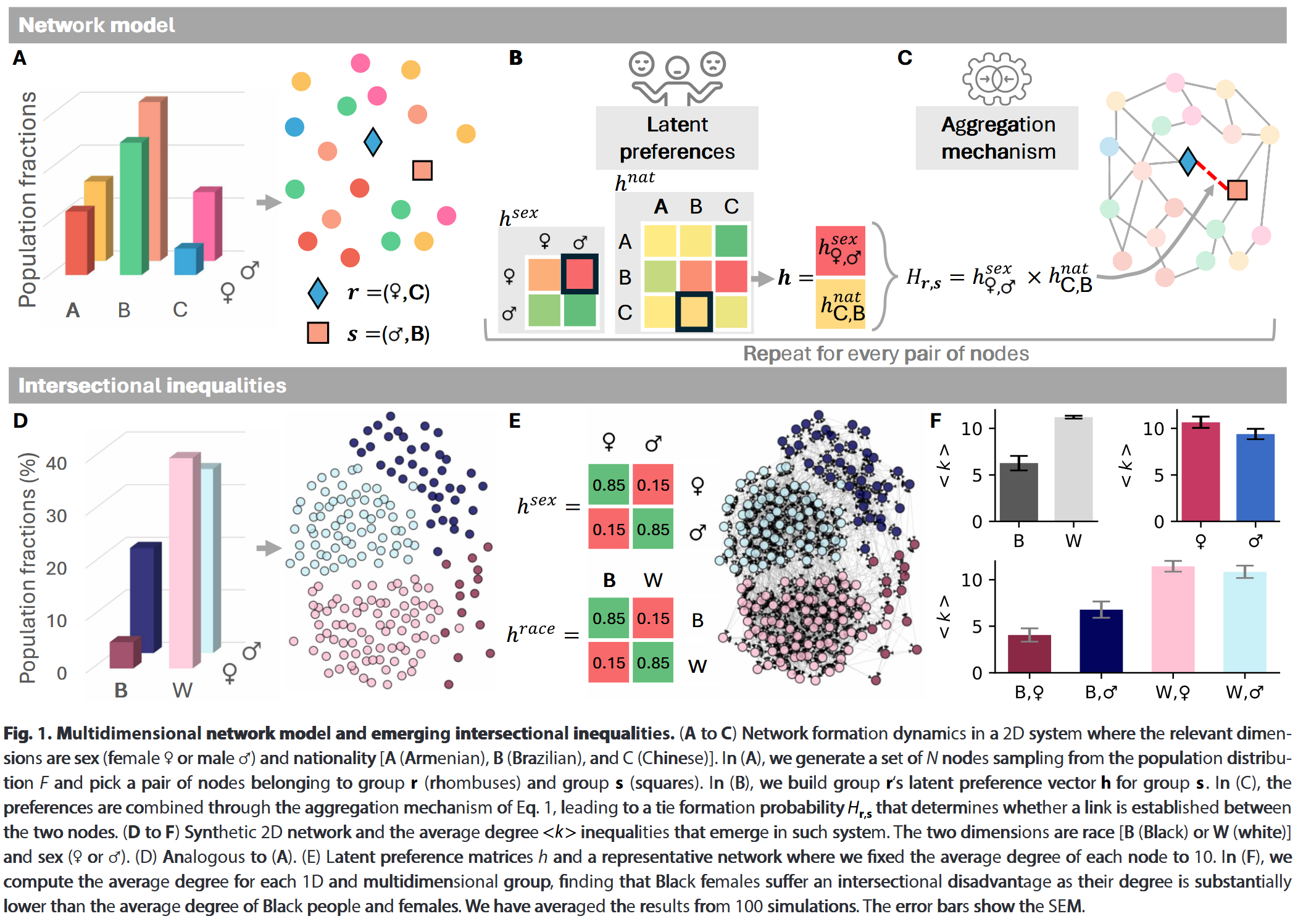
在有向图网络中,边$i\to j$表示节点$i$选择与节点$j$连接。使用入度$k_j$作为节点$j$社会资本的代理
群体间网络不平等源自两个机制:群体规模不平衡与连接偏好偏见。
对于合成数据,作者生成了一个带有预设少数群体规模和相关性的二维二元系统$D=2,v_1=v_2=2$,每个维度中都有一个少数群体$m$和多数群体$M$
总体张量$F=\left[ \begin{array}{cc} F_{m,m} & F_{m,M} \\ F_{M,m} & F_{M,M} \end{array} \right]$,$F_{m,M}$指属于$(m,M)$部分的个体
群体$s^1$在第一个维度的部分为$f_{s^1}^1 = F_{s^1,m} + F_{s^1,M}$群体组$s^2$在第二个维度的部分为$f_{s^2}^2=F_{m,s^2}+F_{M,s^2}$
在二元系统中,维度$d$上的少数群体$f_m^d\leq 0.5$
总体张量可以有两种极端形式,一种在对角线中取值最高,称为最大相关分布distribution of maximum correlation (MC),另一种在反对角线取最高值称为最大反相关分布distribution of maximum anticorrelation (AC)
$F^{MC}=\left[\begin{array}{cc}f_m^1 & 0 \\ f_m^2-f_m^1 & 1-f_m^2\end{array}\right]$ $F^{AC}=\left[\begin{array}{cc} 0 & f_m^1 \ f_m^2 & 1-f_m^2-f_m^1\end{array}\right]$
二维系统中两个维度之间存在相关性,使用参数$\kappa\in[0,1]$控制
使用两个极端形式的线性组合表示任意一个总体:$F=\kappa F^{MC}+(1-\kappa)F^{AC}=\left[\begin{array}{cc}\kappa f_m^1 & (1-\kappa)f_m^1 \\ f_m^2-\kappa f_m^1 & 1-f_m^2 -(1-\kappa)f_m^1\end{array}\right]$
对于属性不相关的总体$F$的元素是对应边际的乘积$F_{s^1,s^2}=f_{s^1}^1f_{s_2}^2$,例如$F_{m,m}=f_m^1f_m^2$
对于每个维度有$v_1, v_2, \cdots, v_D$取值的多维系统,除边缘分布外需要$\prod_{d}V_d-[\sum_dV_d-(D-1)]$个参数来充分定义总体分布。例如对于$D=2;v_1=v_2=2$的系统仅需要一个参数。
为便利性,将$\kappa$缩放为$[0,1]$即$\kappa_{rs}=\left\{\begin{aligned}&\frac{\kappa-f_m^2}{1-f_m^2}\quad if\quad \kappa\geq f_m^2 \\ &\frac{\kappa- f_m^2}{f_m^2}\quad if\quad \kappa<f_m^2 \end{aligned}\right.$
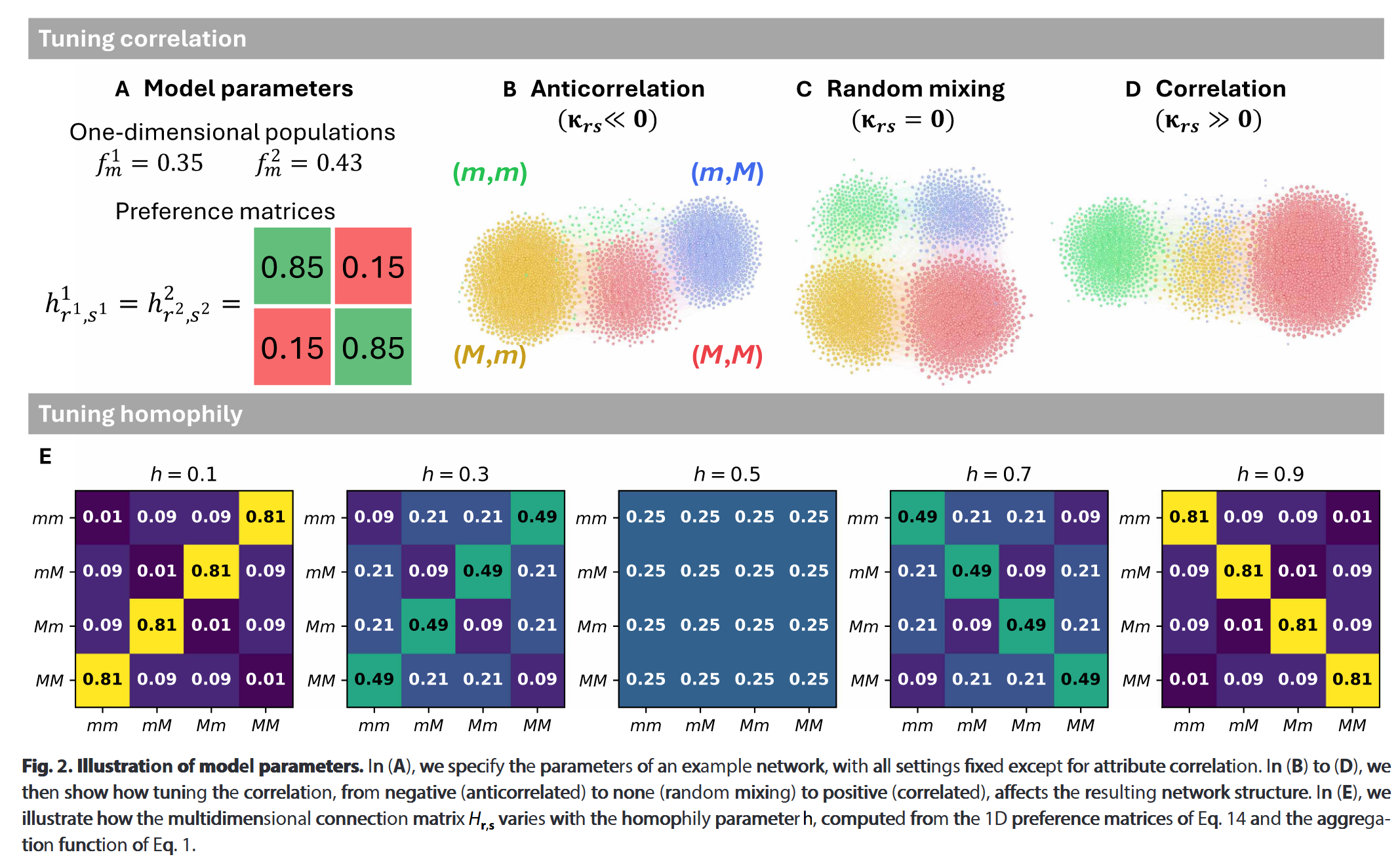
使用度分布之间的随机差stochastic difference衡量群体间的入度差异
令$k_{i\in R}$和$k_{j\in s}$分别表示从群体$R(Rhombuses)$和$S(Squares)$中随机抽取的两个节点的度,当作独立随机变量
-
两个群体的随机差 $\delta_{R,S}=P(k_{i\in R}>k_{j\in S})-P(k_{i\in R}<k_{j\in S})$
-
单个群体的总体差定义为它与其他所有群体的随机差 $\delta_{R}=P(k_{i\in R}>k_{j\notin R})-P(k_{i\in R}<k_{j\notin R})$
指标$\sigma_R\in [-1,+1]$群体的层级,指标越高则群体的特权越高
虽然随机差是一个群体指标,但是它捕获了群内随机个体节点经历的优劣势
作者使用泊松近似推导出一个闭式解析表达式以表达多维群体$r$相较于其他群体$s$的优势
$\delta_{r,s} = Q_1(\sqrt{2\lambda_r},\sqrt{2\lambda_s}) - Q_1(\sqrt{2\lambda_s}, \sqrt{2\lambda_r})$
其中$Q_v(a,b)$是$v$阶the generalized Marcum Q-function,$\lambda_r$是群体$r$的期望入度$\lambda_r=N\sum_s F_s H_{s,r}$
入度不平等取决于偏好$H_{r,s}$总体函数$F_s$和网络规模$N$
利用$\delta$的属性,可推导以下闭式解
两个一维群体的匹配差异$\delta_{r^d,s^d}^d=\frac{1}{f_{r^d}^df_{s^d}^d}\sum_{\begin{aligned}\rho^d=r^d \ \sigma^d=s^d\end{aligned}}F_\rho F_\sigma\delta_{\rho,\sigma}$
一维群体的总体差异$\delta_{r^d}^d=\frac{1}{f_{r^d}^d(1-f_{r^d}^d)}\sum_{\begin{aligned}\rho^d= r^d \ \sigma^d\neq s^d\end{aligned}}F_\rho F_\sigma\delta_{\rho,\sigma}$
多维总体差异$\delta_r=\frac{1}{1-F_r}\sum_{\sigma\neq r}F_\sigma \delta_{r,\sigma}$
模拟实验
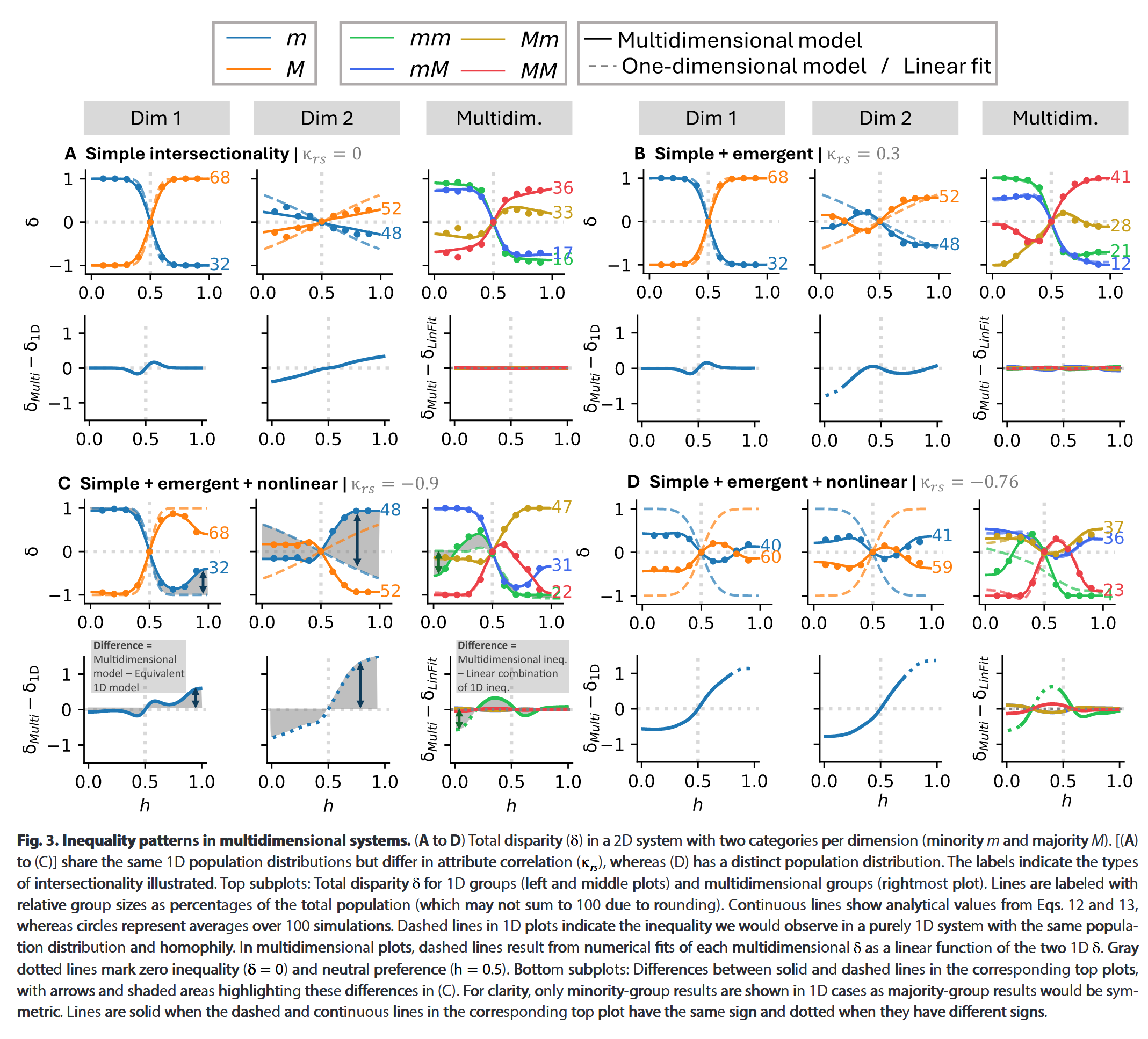
考虑$M$为该属性下的优势群体,$m$为劣势群体;$h$为偏好参数(横坐标)
-
当属性不相关时,连接不平等特性相对简单,较大的群体在同质性($h>0.5$)条件下较为有利,较小的群体在异质性($h<0.5$)下更有利
-
若满足 $h>0.5$ ,则社会资本总体差指标 $\delta_{MM}\geq\delta_{Mm}\geq\delta_{mM}\geq\delta_{mm}$
- 若满足 $h<0.5$ ,则社会资本总体差指标 $\delta_{mm}\geq\delta_{mM}\geq\delta_{Mm}\geq\delta_{MM}$
- 多维度是单维度的简单交叉
-
-
在一维层面存在两种类型的偏离
- 一个群体同时在同质/异质光谱两端都获得优势
- 多数与少数群体在两端区域翻转
在多维系统且属性相关时:
| $\kappa_{rs}$ | 偏好 | 图像 | 描述 |
|---|---|---|---|
| 0.3 | 异质性偏好 $h<0.5$ | 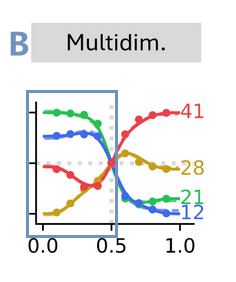 |
$mm$ 群体(21%)比较小的 $mM$ (12%)有优势,因为最大群体 $MM$ (41%)偏好 $mm$ [?总体102%] |
| -0.9 | 同质性偏好 $h>0.5$ | 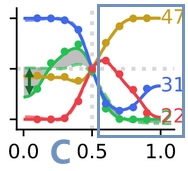 |
较小群体 $MM$ (22%)在多数范围内比较大群体 $mM$ (31%)有优势,因为最大群体 $Mm$ (47%)对 $MM$ 有更强的同质性偏好,且 $mm$ (2%)很小 [?总体102%] |
| -0.76 | 极端异质性偏好 $h\ll 0.5$ | 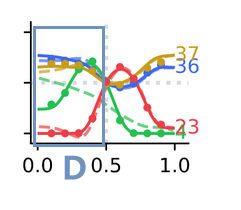 |
两个最大群体 $mM$ 与 $Mm$ 有最大的优势,因为在 $h<0.5$ 条件下二者有强烈的相互偏好 |
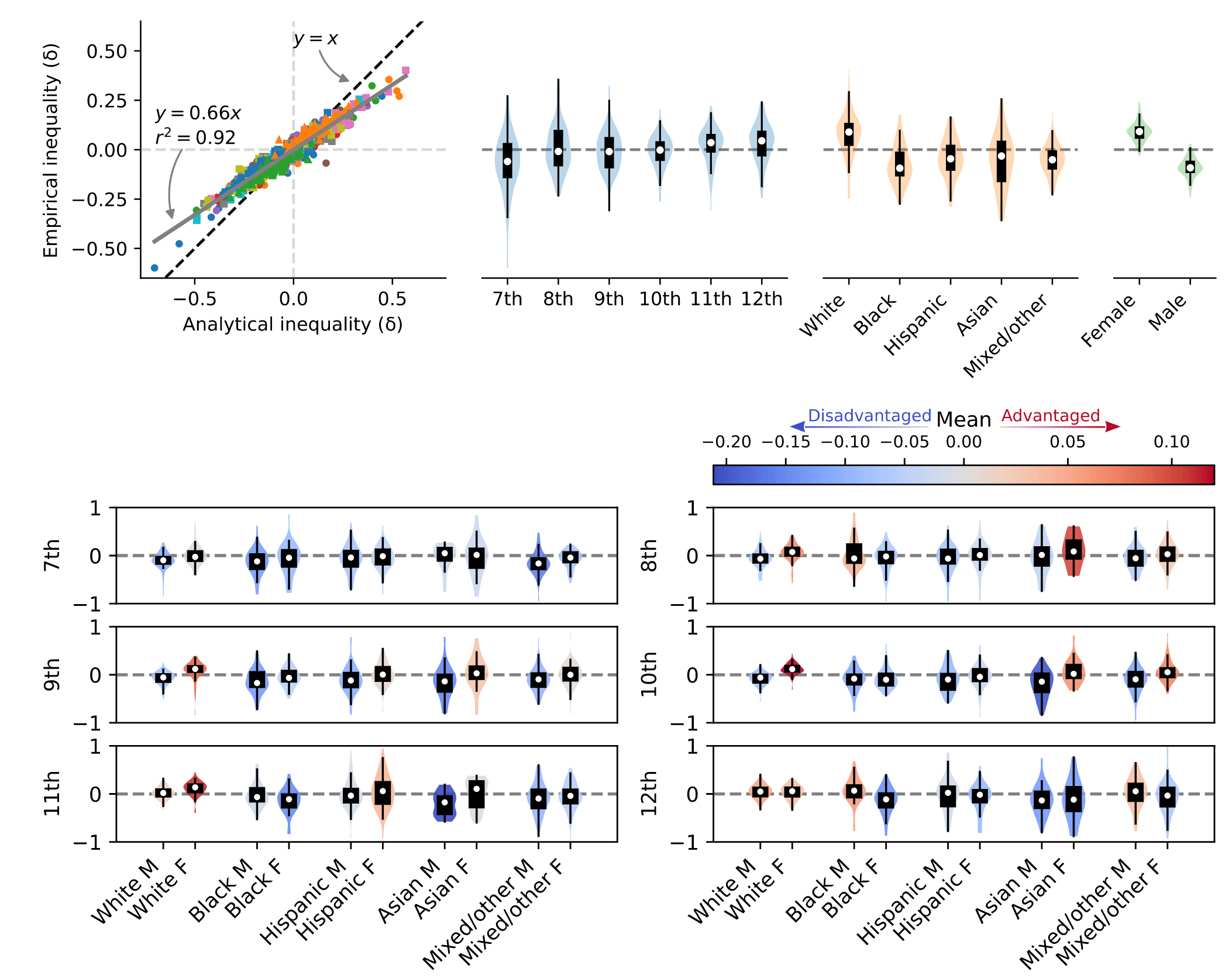
实证实验
使用the National Longitudinal Study of Adolescent Health (AddHealty) 数据集,包含美国高中友谊关系及学生的社会统计属性
娱乐
Quantifying Information Distribution in Social Networks: The Structural Entropy Index of Community (SEIC) for Twitter Communication Analysis 3
这篇文章试图基于香农熵结合图论、社会网络分析构建新的网络结构度量指标:社区结构熵指数SEIC,分析社区的中心化程度。但是这篇文章设计的指标我认为未能论证SEIC与传统的分析指标HHI、Gini等指标的优势与差异,仅论证了它们是一类相关的指标。作者提出的一些指标优势论证不够扎实,或完全可以通过简单的结合其他指标更好地实现。
香农熵$H=-\sum\limits_{i=1}^n p_i log_2 p_i$,其中$p_i$ 表示事件$i$的观测概率,在网络科学中通常被解释为网络节点的归一化活动度或度数。高熵意味着平衡、多样化的社区结构;低熵意味着层级或中心化的交互。
社区结构熵指数 the Structural Entropy Index (SEIC)
令$C\subseteq V$定义为一个由一组节点表示的被检测社区;$dev(v)$ 表示社区内节点$v\in C$的社区内的度。$C$内归一化度分布$p_v= \frac{deg(v)}{\sum_{u\in C} deg(u)}$;其中$p_v$表示随机选择一条社区内的边与节点$v$相连的概率。社区$C$内的香农熵定义为$H_C=-\sum_{v\in C}p_v log_2 p_v$ 用来量化社区内社区活动的多样性或不确定性。将社区香农熵归一化得到社区结构熵指数$SHIC(C)=\frac{H_C}{log_2|C|}$;当指数接近1时表示去中心化社区,接近0表示科层制或垄断交互模式;归一化保证了不同规模的社区可比。
Benchmark
| 指标名称 | 描述 | 数学公式 | 优缺点 |
|---|---|---|---|
| 社区标准化HHI | 用于衡量社区内集中度的指标 | $\widetilde{HHI}(C)=\frac{\sum_{v\in C} p_v^2 - 1/|C|}{1-1/|C|}$ | |
| 标准化Gini系数 | 计算交互强度${x_v}$并用有限样本标准化 | ||
| Modularity Q | 用于衡量社区结构的凝聚性,Q值越高说明网络中社区内部连接越紧密、社区间连接越稀疏,社区划分越明显。通常用于无真实社区标签时,评估社区检测算法的效果(如 Louvain、Girvan-Newman 算法的结果),快速筛选有潜在社区结构的网络 | $Q= \frac{1}{2m}\sum_{i,j=1}^n(A_{ij}- \frac{k_i k_j}{2m})\delta (c_i,c_j)$ | 优点:衡量社区内部连接紧密程度;缺点:对大型网络中的小社区不敏感,对社区数量不敏感 |
| Normalized Mutual Information (NMI) | 对社区数量不敏感,标准化后可以跨数据集、跨算法比较,鲁棒性强,对少量错误标签不敏感 | $NMI(U,V)=\frac{MI(U,V)}{F(H(U), H(V))}$,其中 $MI(U,V)=\sum_{i=1}^R\sum_{j=1}^C p_{i,j} \log(\frac{p_{i,j}}{p_i\times p_j})$,$F(x_1, x_2)$ 可以为几何平均 $\sqrt{x_1x_2}$ 或算术平均 $\frac{x_1+x_2}{2}$ | 优点:标准化后可跨数据集比较,鲁棒性强;缺点:依赖真实标签,当社区数量极多或极少时熵值趋近于0导致指标偏差 |
| Variation of Information (VI) | 核心逻辑是计算检测划分与真实划分的联合熵与互信息的差,衡量两个划分中不共享的信息总量 | $\begin{aligned}VI(X,Y)=&H(X)+H(Y)-2\cdot MI(X,Y) \\ &=H(X|Y)+H(Y|X)\end{aligned}$ |
Proximity to explosive synchronization determines network collapse and recovery trajectories in neural and economic crises 4
| SPL | ROF | 度量 | 模型 |
|---|---|---|---|
| 大脑和金融市场等复杂系统通常处于临界状态,这种状态持续灵活高效的功能,但容易受到严重干扰 | 爆炸性同步接近度更高的网络更容易受到扰动,更容易失去临界态 | 临界点识别:PCF (the pair correlation function) 峰值 | Modified Stuart-Landau Model |
| 自然界中大多数系统经历连续(二阶)跃迁,但有些系统接近一种称为爆炸同步 (ES) 的不连续一阶跃迁 | 由于其内部韧性和双稳定性,这些网络在扰动停止后需要更长的恢复时间 | ES接近度:接近度更高的网络其连续ACF值的变异性更大,导致ACF分布出现厚尾特征;采用滑动窗口获取连续的ACF序列,计算其分布峰度作为ES测量 |
一阶相变 first order phase transformation
在相变点,系统的某些物理量函数本身是连续的,但一阶导数是不连续的
典型案例是冰的融化和水的汽化
爆炸性同步ES
属于特殊的一阶相变,系统从无序状态到同步状态的转变呈现突然且不连续的跳跃,在瞬时间形成大规模同步集团。ES本质可以理解为“抑制规则”,在临界值之前,抑制规则阻止小同步簇合并,维持多个独立小同步集团;到达临界值时,抑制规则突然时效,所有小簇瞬间合并形成巨大同步集团
二阶相变 second order phase transformation (连续相变)
若函数和它的一阶导数在相变点是连续的,但二阶导数不连续,有跃变。经典案例包含超导、超流等
分岔理论 56
分岔理论Bifurcation Theory是研究一群曲线在本质或拓扑结构上的改变。一群曲线可能是向量场内的积分曲线,也可能是一群类似的微分方程的解。
具体地说,针对非线性系统的多重平衡特性,分岔指外界条件(如$r$)发生变化后对系统行为特征产生的质的改变,如定态的产生或消失;稳定性的改变;定态类型、个数或空间分布的改变。
- 定态(不动点 focus node center saddle)
- 稳定定态:施加扰动后运动偏离量始终有界
- 半稳定定态half-stable fixed point
- 不稳定定态
- 周期解/ 极限环 limit cycle
- 稳定
- 不稳定
- 单侧稳定
- 吸引子 attractor
- 吸引域 basin of attraction
$.{x}$为$\frac{d x}{d t}$
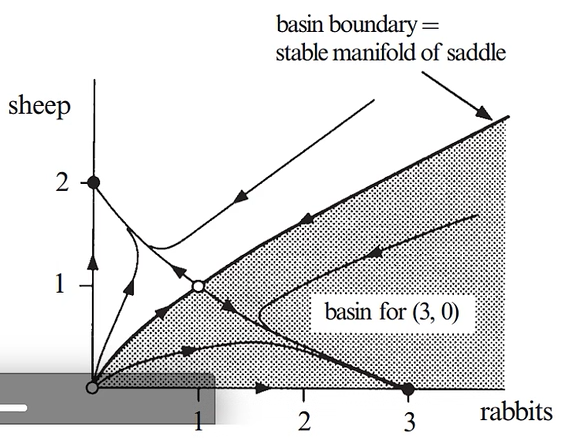
兔羊模型 (属于Lotka-Volterra Model 竞争关系种群动力学)
假设:相同的食物供给,有限的生存空间
模型:单物种增长规律;物种间相互作用
$.{x}=x(3-x-2y)$ $x$: 兔的数量
$.{y}=y(2-x-y)$ $y$: 羊的数量
共有四个不动点,两个$(0,2); (3,0)$是稳定的;阴影和空白分别是两个吸引子的吸引域
一维系统的典型分岔
$x_{fixed}-r$ 坐标图为Bifurcation Diagram
图中稳定性或不动点的变化点称为Bifurcation Point
图中箭头代表施加扰动后变化量的方向,实心点为稳定不动点
- 鞍点-结点分岔
不动点的数量发生改变

- 跨临界分岔
不动点的稳定性发生改变
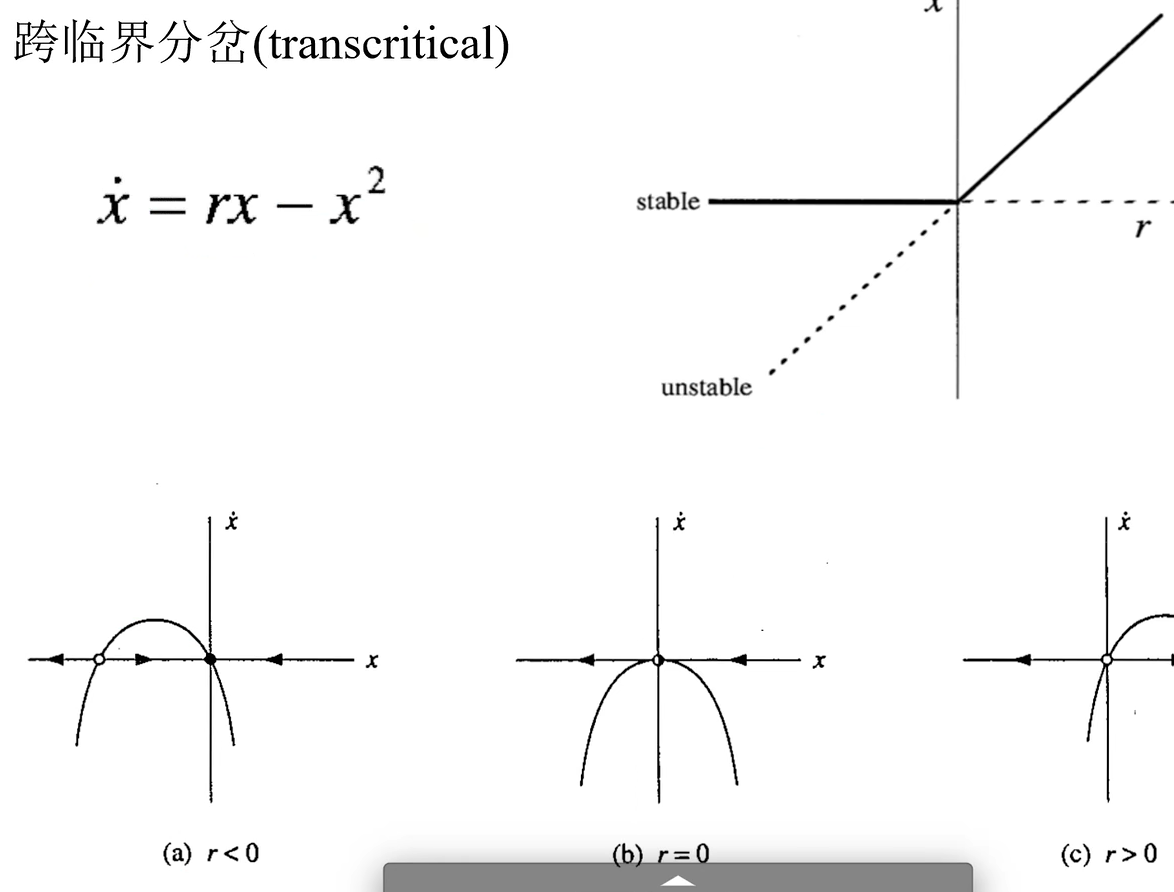
- 超临界分岔
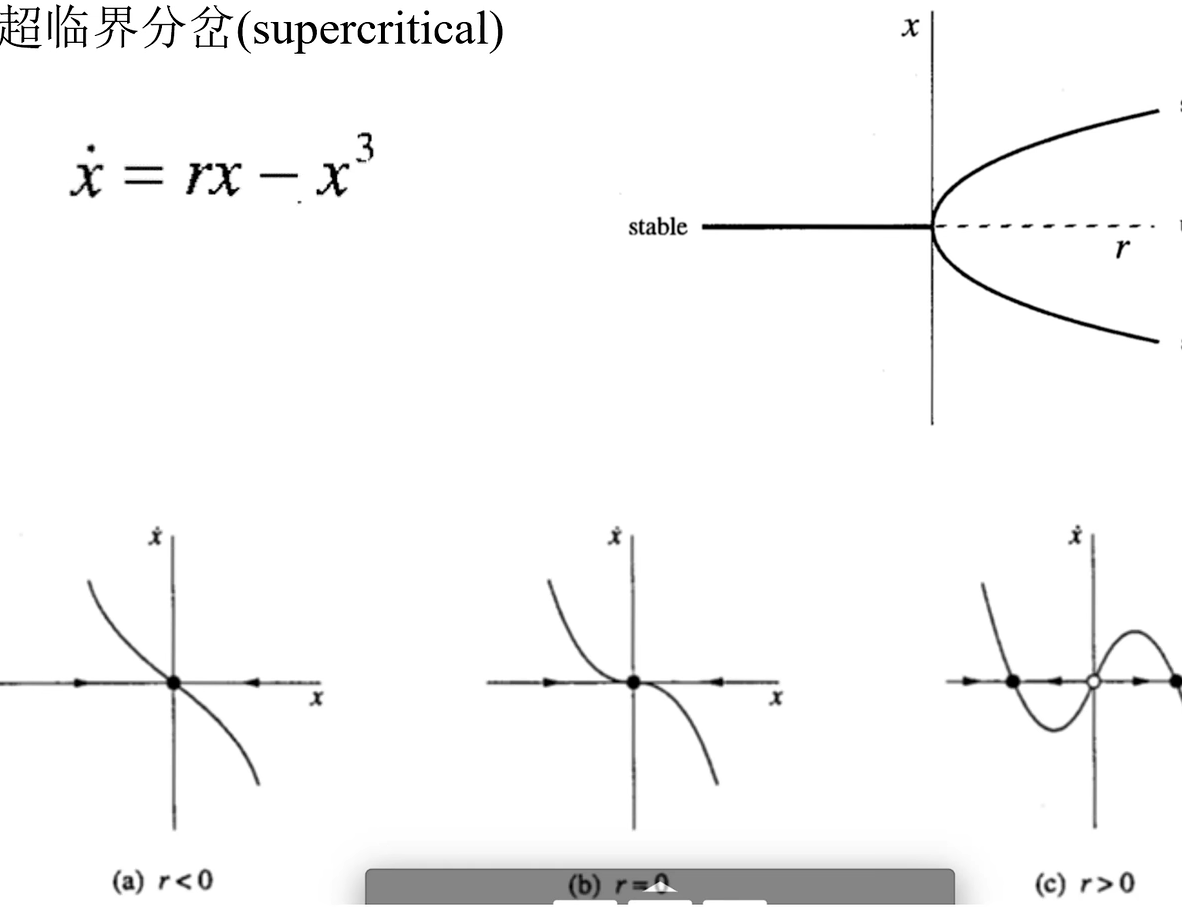
分岔的特性
- Locked-in 锁定:需要较大的扰动才能逃逸当前状态
- Path Dependence:在特定状态下面临的选择受到过去的状态限制,即使这些过去的状态不再相关
共有四个不动点,两个$(0,2); (3,0)$是稳定的;阴影和空白分别是两个吸引子的吸引域
一维系统的典型分岔
$x_{fixed}-r$ 坐标图为Bifurcation Diagram
图中稳定性或不动点的变化点称为Bifurcation Point
图中箭头代表施加扰动后变化量的方向,实心点为稳定不动点
- 鞍点-结点分岔
不动点的数量发生改变

- 跨临界分岔
不动点的稳定性发生改变

- 超临界分岔

分岔的特性
- Locked-in 锁定:需要较大的扰动才能逃逸当前状态
- Path Dependence:在特定状态下面临的选择受到过去的状态限制,即使这些过去的状态不再相关

The Hopf Bifurcation 7
在Hopf分岔点,平衡点的稳定性发生变化,从该平衡点分岔出一个唯一的周期性极限环

- 超临界Hopf分岔 Supercritical Hopf Bifurcation:当 $\mu>\mu_0$ 时,分岔出稳定的极限环,原平衡点失去稳定性
- 亚临界Hopf分岔 Subcritical Hopf Bifurcation:当 $\mu<\mu_0$ 时,分岔出不稳定的极限环并向一个稳定的不动点坍缩,导致极限环消失和一个不稳定的不动点
Stuart-Lanau 模型
该模型是超临界Hopf分岔邻域内非线性动力系统的低维有效降阶模型,能够以极简的形式捕捉系统从稳态到周期性极限环震荡的动力学行为
本研究:Modefied Stuart-Lanau Model
$\begin{aligned} \dot{z}_j=&\{\lambda_j + i \omega_j - |z_j(t)|^2\}z_j(t)+R_j^ZS\sum_{k=1}^NA_{jk}K_{jk}z_j(t-\tau_{jk})+\beta\xi_j(t)+u(t),\\ &j=1,2,…,N\quad u(t)=\left\{ \begin{array}{rcl}p,t_1<t<t_2 \\ 0,otherwise\end{array} \right. \end{aligned}$
模型中,网络的每个节点使用复杂变量$z_j=r_je^{i\theta_j}$表示,其中$r_j$和$\theta_j$ 是振子$j$的振幅和相位 (极坐标能够直接映射两个变量关系)
$\lambda_j$ 为振子$j$ 的振幅衰减率,$w_j$为振子$j$的自然频率
$-|z_j(t)^2|$ 为用于描述振子自反馈效应的非线性项,当振子的振幅增大时该项限制振子的振幅;对于复数的模$|z_j|=r$,因此$|z|^2z=r^3e^{i\theta}$,与自身状态$re^{i\theta}$同相位(即仅影响强度,不影响节奏)
$A_{jk}$ 连接矩阵,表示节点$j$和节点$k$之间的连接关系,1表示存在连接,0表示没有连接;$K_{jk}$偶合强度,表示节点$j$和节点$k$之间的相互作用强度;$\tau_{jk}$时间延迟,表示从节点 $k$ 到节点 $j$ 的信号传输时间延迟,用于模拟实际网络中的信号传播延迟;$R_j^Z$自适应反馈项表示节点间的递归交互,$Z$与ACF分布峰度相关
$\xi_j(t)$高斯白噪声,捕捉系统的随机波动,实验中噪声强度$\beta$固定为0.05
$u(t)$外部刺激,一个全局的脉冲刺激,刺激强度为$p$,持续时间为$T=t_2-t_1$
Discovering sensorimotor agency in cellular automata using diversity search 8
Survival Tips9
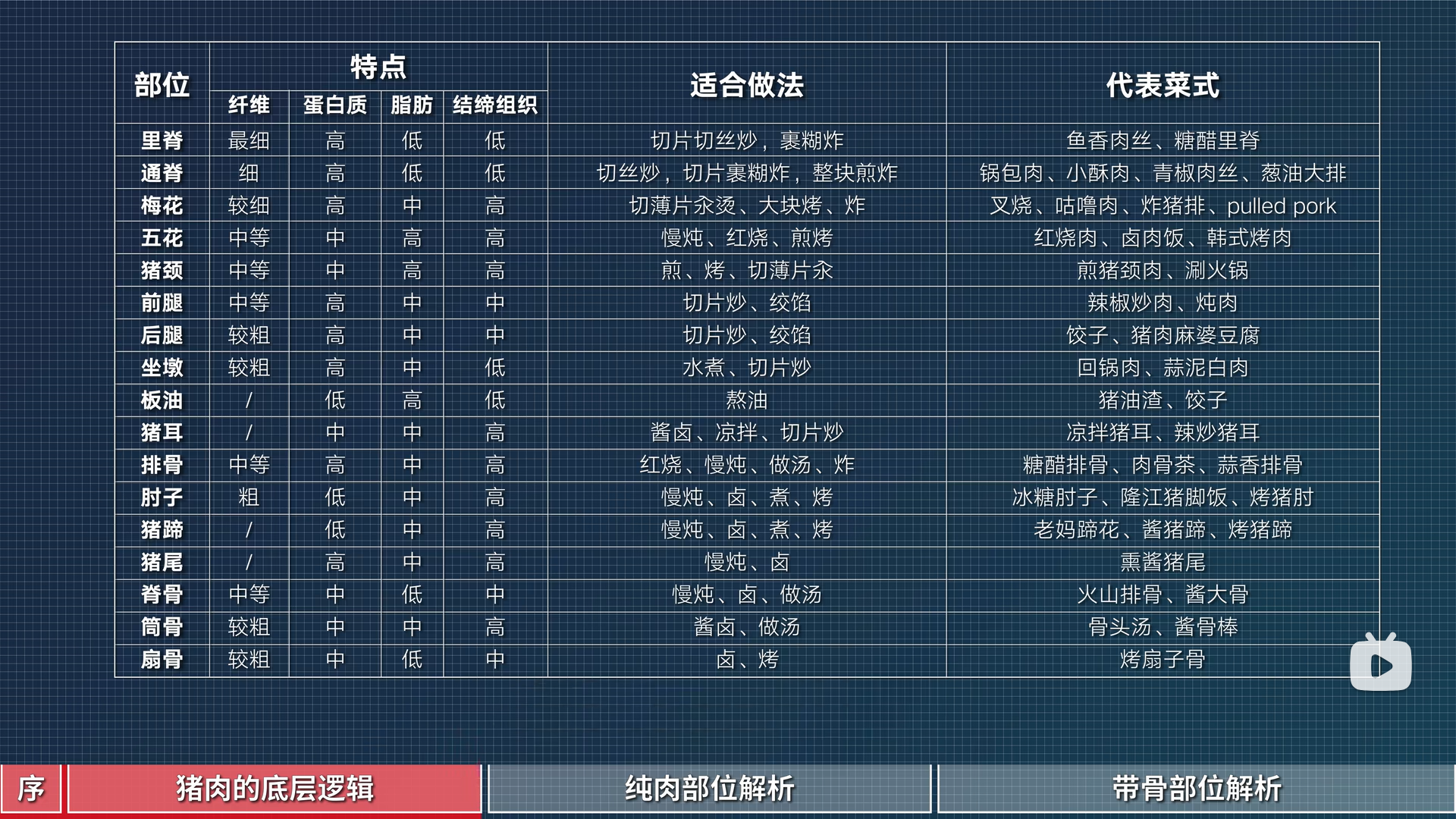
-
Guan, H., He, J., Fan, L., Ren, Z., He, S., Yu, X., Chen, Y., Zheng, S., Liu, T.-Y., & Liu, Z. (2025). Modeling earth-scale human-like societies with one billion agents (No. arXiv:2506.12078). arXiv. https://doi.org/10.48550/arXiv.2506.12078 ↩
-
Martin-Gutierrez, S., Cartier Van Dissel, M. N., & Karimi, F. (2025). Intersectional inequalities in social ties. Science Advances, 11(45), eadu9025. https://doi.org/10.1126/sciadv.adu9025 ↩
-
Błocki, W., Szewczyk, M., & Adamski, A. (2025). Quantifying Information Distribution in Social Networks: The Structural Entropy Index of Community (SEIC) for Twitter Communication Analysis. Entropy, 27(11), 1140. https://doi.org/10.3390/e27111140 ↩
-
Lee, U., Kim, H., Kim, M., Oh, G., Joo, P., Park, A., Pal, D., Tracey, I., Warnaby, C. E., Sleigh, J., & Mashour, G. A. (2025). Proximity to explosive synchronization determines network collapse and recovery trajectories in neural and economic crises. Proceedings of the National Academy of Sciences, 122(44), e2505434122. https://doi.org/10.1073/pnas.2505434122 ↩
-
李红刚_Bnu. (n.d.). Ss72【动力系统分岔理论】_哔哩哔哩_bilibili. Retrieved November 19, 2025, from https://www.bilibili.com/video/BV1SMspeAE5R/ ↩
-
羽生扶苏. (n.d.). 徒手撸公式 讲解分岔理论丨introducing bifurcations——The saddle node bifurcation_哔哩哔哩_bilibili. Retrieved November 19, 2025, from https://www.bilibili.com/video/BV1PP4y1Y7jP/ ↩
-
Hopf bifurcations—Dynamical systems _ lecture 26_哔哩哔哩_bilibili. (n.d.). Retrieved November 20, 2025, from https://www.bilibili.com/video/BV1tw411s77w/?spm_id_from=333.1007.top_right_bar_window_default_collection.content.click&vd_source=3a2d88cb18aadffe0dabe9dd1ee84683 ↩
-
Hamon, G., Etcheverry, M., Chan, B. W.-C., Moulin-Frier, C., & Oudeyer, P.-Y. (2025). Discovering sensorimotor agency in cellular automata using diversity search. Science Advances, 11(44), eadp0834. https://doi.org/10.1126/sciadv.adp0834 ↩
-
杨光_建厨师. (n.d.). 底层逻辑解构猪肉,理解各部位的区别和做法,不用死记硬背_哔哩哔哩_bilibili. Retrieved November 21, 2025, from https://www.bilibili.com/video/BV1Ni2PBMEmm/ ↩